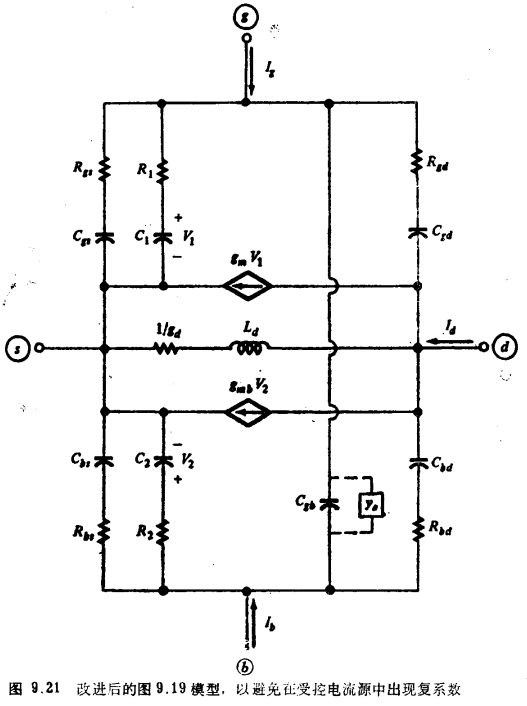
MOS晶体管非准静态模型的比较原理特性解析图9.23表示了a=0.5(VDS=V´DS／2)，强反型时,∣m∣/gm和m的相位与频率(对数标尺)的关系曲线。频率ω0由式(8.3.6)给出，为方便起见重写于此：在每一图中，曲线a对应于图8.13的简单摸型，曲线b对应于图9.5的完整准静态模型，曲线c对应于图9.19或图9.21模型。MOS晶体管非准静态模型的比较。最后，曲线d对应于在式（9.4.65
MOS晶体管非准静态模型的比较原理特性解析图9.23表示了a=0.5(VDS=V´DS／2)，强反型时,∣m∣/gm和m的相位与频率(对数标尺)的关系曲线。频率ω0由式(8.3.6)给出，为方便起见重写于此：在每一图中，曲线a对应于图8.13的简单摸型，曲线b对应于图9.5的完整准静态模型，曲线c对应于图9.19或图9.21模型。MOS晶体管非准静态模型的比较。最后，曲线d对应于在式（9.4.65
MOS晶体管非准静态模型的其他近似法和高阶原理特性解析如上所述，本节中导出的模型在频率高到ω=ω0左右时都是有效的。在推导这一模型中，我们采用了一种特定类型的近似，例如用式(9.4.69a)近似式(9.4.65a)。人们也许想知道为什么不简单地略去式(9.4.65a)中的高次项，即不经任何进一步处理就使用-gs=jωCgs（1+jωτ1）。MOS管非准静态模型。答案是这样一种方法并不明智，原因有两
MOS晶体管非准静态模型的其他近似法和高阶原理特性解析如上所述，本节中导出的模型在频率高到ω=ω0左右时都是有效的。在推导这一模型中，我们采用了一种特定类型的近似，例如用式(9.4.69a)近似式(9.4.65a)。人们也许想知道为什么不简单地略去式(9.4.65a)中的高次项，即不经任何进一步处理就使用-gs=jωCgs（1+jωτ1）。MOS管非准静态模型。答案是这样一种方法并不明智，原因有两
MOS晶体管非准静态模型的复指数激励原理特性解析我们可以假设小信号电压是正眩的，并认为对应的小信号端电流处于正弦稳态。但是，结果发现代数运算是不必要的复杂。因此，我们将仿照一种标准的做法，改为研究一个假想的复指数形式的激励：其中带小写下标的大写字母表示与时间无关的，通常是复数的相量，ω是角频率(以rad／s为单位)。MOS管非准静态模型的复指数激励。由于联系各种小信号量的方程(上面导出的)是线性的
MOS晶体管非准静态模型的复指数激励原理特性解析我们可以假设小信号电压是正眩的，并认为对应的小信号端电流处于正弦稳态。但是，结果发现代数运算是不必要的复杂。因此，我们将仿照一种标准的做法，改为研究一个假想的复指数形式的激励：其中带小写下标的大写字母表示与时间无关的，通常是复数的相量，ω是角频率(以rad／s为单位)。MOS管非准静态模型的复指数激励。由于联系各种小信号量的方程(上面导出的)是线性的
MOS晶体管非准静态模型的小信号激励原理特性解析现在假设总的端电压具有下面的形式：每式中右边的第一项是偏置电压，第二项是小信号电压(所有小增量都用小写下标来表示)。采用上述电压形式的结果是使分析中的其他时变量的形式为：假设υgs(t)、υbs(t)和υds(t)很小，上述用大写字母和大写下标表示的所有量都将和直流激励下的量一样；它们的值已经求得。把由式(9.4.29)和式(9.4.30)得到的量代
MOS晶体管非准静态模型的小信号激励原理特性解析现在假设总的端电压具有下面的形式：每式中右边的第一项是偏置电压，第二项是小信号电压(所有小增量都用小写下标来表示)。采用上述电压形式的结果是使分析中的其他时变量的形式为：假设υgs(t)、υbs(t)和υds(t)很小，上述用大写字母和大写下标表示的所有量都将和直流激励下的量一样；它们的值已经求得。把由式(9.4.29)和式(9.4.30)得到的量代
MOS晶体管非准静态模型的时变激励原理特性解析我们将用带大写下标的小写字母表示总的(大信号)量。MOS管非准静态模型的时变激励。下面指出，在时变电压(时间相关性全部以显式表明)情况下，式(9.4.2)至式(9.4.7)必须这样修正：其中Q´o假定固定不变。式中式（9.4.9）必须用下式来代替因为我们要考虑电压快速变化，眼下，式(9.4.10)还没有一个相应于这种情况的公式。所以，我们必须改用“连续
MOS晶体管非准静态模型的时变激励原理特性解析我们将用带大写下标的小写字母表示总的(大信号)量。MOS管非准静态模型的时变激励。下面指出，在时变电压(时间相关性全部以显式表明)情况下，式(9.4.2)至式(9.4.7)必须这样修正：其中Q´o假定固定不变。式中式（9.4.9）必须用下式来代替因为我们要考虑电压快速变化，眼下，式(9.4.10)还没有一个相应于这种情况的公式。所以，我们必须改用“连续
MOS晶体管非准静态模型工作原理及其特性解析本节将要导出个对应于近似强反型直流模型的，有用的高频漠型。为了最后得到易处理的表达式，这里将要采用与8.3节巾相同的简化假设。第一条假设是：电荷表达式中的δ假设为 第二条假设是：就我们的目的而言，δ1对VS或VB的导数可以忽略，因此在微分是δ1将作为常数处理。MOS晶体管非准静态模型。以后我们将通过与更准确的模型进行比较，证明从上述假设确实得出一个有用
MOS晶体管非准静态模型工作原理及其特性解析本节将要导出个对应于近似强反型直流模型的，有用的高频漠型。为了最后得到易处理的表达式，这里将要采用与8.3节巾相同的简化假设。第一条假设是：电荷表达式中的δ假设为 第二条假设是：就我们的目的而言，δ1对VS或VB的导数可以忽略，因此在微分是δ1将作为常数处理。MOS晶体管非准静态模型。以后我们将通过与更准确的模型进行比较，证明从上述假设确实得出一个有用
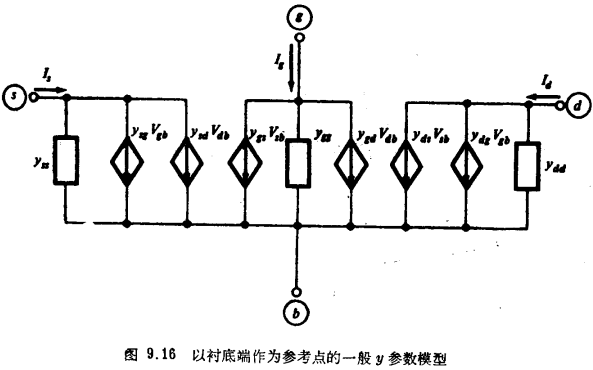
讲解MOS晶体管参数模型工作原理图及其特性超高频放大器（并非必须使用MOS晶体管）的设计常常利用所谓参数来进行。本节中我们推导关于MOS器件的参数模型。我们将首先推导出这种模型的一般形式。进行这一推导时，对器件的物理情况将不作任何假设。MOS晶体管y参数模型。事实上，我们甚至不必假设器件是一个MOS晶体管。对器件设置的唯一限制条件是它有四个端子。为了以后方便，我们将用D、G、B和S来表示这些端子。
讲解MOS晶体管参数模型工作原理图及其特性超高频放大器（并非必须使用MOS晶体管）的设计常常利用所谓参数来进行。本节中我们推导关于MOS器件的参数模型。我们将首先推导出这种模型的一般形式。进行这一推导时，对器件的物理情况将不作任何假设。MOS晶体管y参数模型。事实上，我们甚至不必假设器件是一个MOS晶体管。对器件设置的唯一限制条件是它有四个端子。为了以后方便，我们将用D、G、B和S来表示这些端子。
解析MOS管高频小信号模型适用的频率范围的特征就所适用的频率范围而论，计入四个电容Cm、Cmb，Cmx和Csd使得完整的准静态模型优于图8.13的简单模型。改善的程度取决于偏压和我们所考虑的端子。例如，饱和时Cm最大，正是在这种情况下，就栅对漏的作用而言，两模型之间的差别最大。当VDS=0时，Cm=0，在这一点上两模型是相同的。另一方面，也正是在VDS=0时，Csd最大， 因此正是在这点上，就源
解析MOS管高频小信号模型适用的频率范围的特征就所适用的频率范围而论，计入四个电容Cm、Cmb，Cmx和Csd使得完整的准静态模型优于图8.13的简单模型。改善的程度取决于偏压和我们所考虑的端子。例如，饱和时Cm最大，正是在这种情况下，就栅对漏的作用而言，两模型之间的差别最大。当VDS=0时，Cm=0，在这一点上两模型是相同的。另一方面，也正是在VDS=0时，Csd最大， 因此正是在这点上，就源
解析MOS管高频小信号弱反型及通用型工作特性弱反型弱反型时唯一重要的本征电容Cgb已在8.3节中讨论过了。推导其他一些本征电容的表达式是不值得的。MOS管高频小信号弱反型。对于所有器件(除沟道很长的器之外)来说，这些电容的效应将被非本征电容的效应所淹没。适用子所有反型区的通用模型利用7.4.5节中提出的精确的电荷计算而导出的电容与VGS的关系曲线示于图9.9。图中画出了用于图9.5模型中的所有九个
解析MOS管高频小信号弱反型及通用型工作特性弱反型弱反型时唯一重要的本征电容Cgb已在8.3节中讨论过了。推导其他一些本征电容的表达式是不值得的。MOS管高频小信号弱反型。对于所有器件(除沟道很长的器之外)来说，这些电容的效应将被非本征电容的效应所淹没。适用子所有反型区的通用模型利用7.4.5节中提出的精确的电荷计算而导出的电容与VGS的关系曲线示于图9.9。图中画出了用于图9.5模型中的所有九个
解析MOS管高频小信号电容计算的强反型工作特性强反型在8.3节中，我们曾用对应于近似模型的电荷表达式来计算五个电容：Cgs、Cbs、Cgd、Cbd和Cgb，并曾给出了这些电容与VDS和BGS的几条关系曲线。MOS管高频小信号电容计算。我们可用同样方法来计算本节中已定义的新电容。MOS管高频小信号强反型。在推导这些电容的表达式时，我们还要利用8.3节中的简化假设，即δ=δ1，δ1由式(8.3.7)给
解析MOS管高频小信号电容计算的强反型工作特性强反型在8.3节中，我们曾用对应于近似模型的电荷表达式来计算五个电容：Cgs、Cbs、Cgd、Cbd和Cgb，并曾给出了这些电容与VDS和BGS的几条关系曲线。MOS管高频小信号电容计算。我们可用同样方法来计算本节中已定义的新电容。MOS管高频小信号强反型。在推导这些电容的表达式时，我们还要利用8.3节中的简化假设，即δ=δ1，δ1由式(8.3.7)给
深圳市龙华区大浪街道浪口社区英泰路8号英泰科汇广场2栋1902
KIA-公众号
Copyright ©2015 广东可易亚半导体科技有限公司
深圳市龙华区大浪街道浪口社区英泰路8号英泰科汇广场2栋1902
KIA-公众号
