MOS晶体管非准静态模型的复指数激励原理特性解析

我们可以假设小信号电压是正眩的，并认为对应的小信号端电流处于正弦稳态。但是，结果发现代数运算是不必要的复杂。因此，我们将仿照一种标准的做法，改为研究一个假想的复指数形式的激励：

其中带小写下标的大写字母表示与时间无关的，通常是复数的相量，ω是角频率(以rad／s为单位)。MOS管非准静态模型的复指数激励。由于联系各种小信号量的方程(上面导出的)是线性的，  所以每一个由式(9.4.49)中的激励在稳态时所产生的效应——小信号量也将等于一个复数乘以e^jωt。具体地说，可以写出

    式(9.4.50)是对式(9.4.49)中激励的各种“响应”。虽然所有这些复激励和复响应都是假想的，但由于下面的原因可知它们是有用的。如果改用上述激励的实部来驱动器件，则所有稳态响应由式(9.4.50)中的假想响应的实部给出。现在，上述任何一个激励的实部都是一个正弦量[例如，若M和Φ分别为Vgs的大小和相位，于是，在式(9.4.49a)中的υgs（t）的实部便是Mcos(ωt+Φ)]。因此若采用上述假想的指数函数来分析问题，则实激励和实响应(只是为了数学上的方便)为正弦稳态提供了一切有用的信息。此外，如果对复指数激励的响应已知，则通过各种变换方法可以确定对其他类波形激励的响应。

现在可以把式(9.4.49)和(9.4.50)中的量代入式(9.4.42)、(9.4.43)、(9.4.40)、(9.4.41)、(9.4.44)，(9.4.46)和(9.4.48)。在所有情况下，e^jωt都作为一个公共因子出现在等号的两边。这样，不难得到

在上述方程中注意下面几点：μ、W、L和C´ox是已知的器件参数，δ₁对应于一给定得偏压VSB，并由式（9.4.1）给定，UI（x）是已给知的由式(9.4.13)给出的x的函数。Vgs、Vbs和Vds是已知的代表激励的相量。MOS管非准静态模型的复指数激励。因此，  对于一给定的ω，式(9.4.51)是关于两个未知函数Ii(x，ω)和Ui(x，ω)的由两个微分方程组成的一个方程组，该方程组可用贝塞尔函数，并结合式(9.4.52)中给定的边界条件来；另一个求解方法是采用迭代技术。函数Ui(x，ω)和Ii(x，ω)一旦确定，就可把它们代入式(9.4.53)以得到Id(ω)、Ig(ω)和Ib(ω)。这里不打算介绍。下面我们概括一下结果的形式，最终表达式为下面这样的形式：

式中，量Nkl(ω)(k，l=d,g,b)和D(ω)是jω的无穷级数。例如

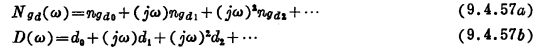
上面两个无穷级数以及式(9.4.54)至(9.4.56)中的所有Nkl(ω)中的一直高到二阶的系数在附录M 中给出。通过把式(9.4.54)至(9.4.56)与式(9.3.8)相比较，最后可以求得参数：

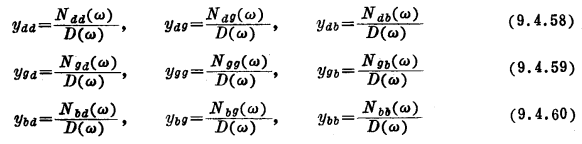
给定一个频率，可以计算参数，通过在分子和分母保留适当数目的项，可使计算结果达到任意要求的精度。这样得到的值可以代入图9.16中的小信号等效电路。

现在考虑图9.17中的等效电路。上面确定的参数中只有三个：gd、gb和bd直接出现在这一电路中，电路中的其余参数可以从式(9.3.7)和式(9.3.10)轻而易举地求得：

式中右边的值由式(9.4.58)至(9.4.60)给出

我们将用有助于把图9.17中的模型与8.3节中导出的模型联系起来的方法，来写图9.17中的模型参数的表达式。现在从式(9.4.58)至(9.4.60)出发进行这一工作。在每一个参数的表达式中，提出分子中第一个不为零的项作为公因子。例如，考虑式(9.4.61)中的gd。

从附录M，有ngd0=0和do=1。这样，我们可以写出

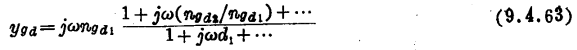
查看附录M发现，-ngd1与式(8.3.10)中的Cgd有完全一样的表达式。因此，我们可以写出

    用类似的方法进行处理，可以求得图9.17中所有参数的表达式。在推导每—表达式时，该表达式中的有一部分可以看成是第8章中讨论过的，大家所熟悉的小信号量。结果概括如下(使用减号，与图9.17对应)：

其中(经过较长的代数运算之后)

式中的a由式(4.4.31)给出，以及

我们注意到，在式(9.4.65f)至(9.4.65h)的分子中，并未包含频率相关的项，这是因为在使用式(9.4.6c)至(9.4.62e)时，这些项互相抵消了。

    现在考虑低频情况，因此ω《ωo。这时，式(9.4.65)给出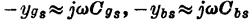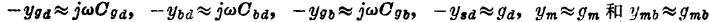。由于这些近似关系及mx=0，图9.17中的模型就简化为图8.13中的模型。这样， 从不同的前提出发得出了相同的模型。

    上述推导中出现的a量由式(4.4.31)给定，且该式中的V´DS=（VGS-VT）/（1+δ），并取δ=δ1。这-δ值用起来并不觉得是最佳的(除非VDS很小)，这一点已在4.4.2节中解释过了。MOS管非准静态模型的复指数激励。但是这里还是出现了这-δ值，因为我们最初用了式(9.4.1)的假定，而这一假设又是获得易处理的结果所必需的。然而，我们还是希望目前的模型能和对应的直流模型，式(4.4.30)一致，直流模型中没有采用δ=δ1的限制。因此，我们将从目前的模型中取消这一限制，而考虑V´DS具有和直流模型式中同样的合适值[见与式(4.4.33)有关的讨论了]。

    类似的评论适用于式(9.4.65)至(9.4.67)中的其他量(Cbs，gb等)。因此，仿照上面所用的方法，可以导出第8章中所熟悉的这些量的表达式，只是δ1用某个不同的量代替而已。[例如，我们求得gmb=b1gm，此式具有式(8.2.10)的形式，但b=b1，b1来自式(8.2.12)，当VDS较大时，正如式(8.2.12)后面所指出的那样，这是不精确的。还有，因为我们没有计入沟道长度调制效应，所以在饱和区，由上述推导得出的gd值为零。通过采纳下面的方法，可以取消所有这样一些限制：第8章中已经遇到过的式(9.4.65)至(9.4.67)中的任意一个量都假设具有那章中所给定的值。这样，在低频时，目前的模型不仅在拓扑上(图8.13)，而且在其元件值上都将简化为8.3节中的模型。这是一个十分希望具有的特性。它使我们有可能把已知的在低频小信号参数方面所作的一切精心的处理结合到目前的模型中来。MOS管非准静态模型的复指数激励。这样，在低频时，模型的特性将会非常好(当然，在低频模型失效的频率上，它也将提供有用的结果)。

    利用式(8.3.15)和(9.4.65)，可得到

如VDS较小，和／或VSB较大，此时，耗尽区沿沟道是近似均匀的，则式(9.4.68)成立，并有良好的精度。在其他情况下，这一关系也成立，但精度是有限的。

现在来推导式(9.4.65)中那些关系式的一些十分有用的近似式。以gs为例。如果工作频率满足ωτ《1，则可以写1+jωτ2≈1／(1-jωτ₂)。把此式代入式(9.4.65a)，并忽略高次项，可得-gs≈jωCgs／[1+jω(τ1-τ2)]；对于-bs,-gd和-bd也类类似。至于这些近似式的有效性，下面很快就要讨论。这样，便有：

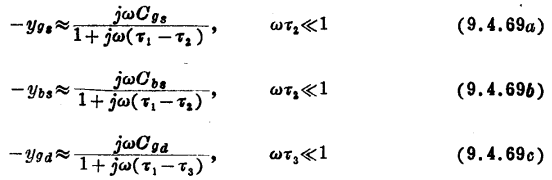
 遗憾的是，这类近似式不能用于-gb。不能在所有偏压下都假设ωτ₄《1，因为当VDS=0(a=1)时，从式(9.4.66d)可见，τ₄变成无限大。[这是因从式(9.4.65a)中提取因子Cgb而引起的人为结果；不难检查，乘积Cgbτ₄的性能是好的。因此，我们将用

 饱和时，在我们所作的另外一些近似是准确的那些频率上，含有(jω)²的项可以略去而影响很小。非饱和时，尤其在VDS非常小的情况下，这一项在gb中可能是主要的一项，但无论如何gb的模值是很小的。它所贡献的小电流几乎不变，且被其他更大的电流(例如，非本征的栅-衬底电容中的电流)所掩盖。因此，对于许多应用来说，含有(jω)²的项可以略去。

    对于式(9.4.65)中的其他参数，我们只是略去分母中的高次项，即

式(9.4.69a)至(9.4.69d)中，等号右边导纳的一般形式为jωC(1+jωτ)。  图9.18a表示了实现这样一个导纳的一种简单电路。图9.18b是实现式(9.4.69f)等号右边导纳的电路，最后，图9.18c表示了实现式(9.4.69e)等号右边导纳的电路，R是任意的。方框内的部分代表含有（jω）²的这一项。MOS管非准静态模型的复指数激励。图9.18中的三种电路表示，可以通过简单的电路分析来证明。

借助于图9.18，不难看出，如果利用式（9.4.69），则图9.17的等效电路取决于图9.19中的形式。虚线方框部分和图9.18c中的一。在许多应用中，由于上面已提到过的原因，该方框部分可以略去。正如从图9.18a和式（9.4.69a）至（9.4.69d）可得到出的那样，有

从上式可以计算出电阻值。正如从图9.18c和式(9.4.69f)可得出的那样，对于电感，有

电阻和电感曲线示于图9.20。

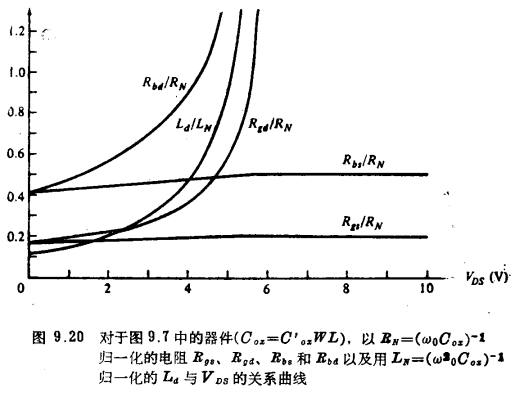
不管式(9.4.69)中ωτ₁《1这—形式的条件是否成立，我们发现刚才介绍的模型一直到ω=ω₀左右都是令人满意的。各种模型的比较将在9.5节中进行。

可以认为图9.19中的各个电阻和那个电感(与和它们相串联的元件协同一起)是代表反型层对于快速变化响应时的惯性所引起的一些效应。这样，如果源电压变化很快，则反型层在响应时显得“犹豫”，栅电流和衬底电流的相应变化也将滞后于源电压的变化；上述效应分别由R_gs、C_gs和R_bs、G_bs来模拟。串联组合R_gd、C_gd和R_bd、C_bd则是模拟漏端电压快速变化时，与上述相应的效应(在非饱和区)。  Ld和gd的串联组合可以认为是代表漏端电压快速变化要求源端电流也有这样快的变化时，反型层所表现的惯性(在非饱和区)。最后，两个电流源分母的值模拟当栅或衬底电压变化时，在改变漏端电流方面反型层所表现的惯性。

如果加在端子上的小信号电压的频率变得足够低，则前面提到的惯性就可忽略。实际上，随着频率的降低，Cgs、Cbs、Cgd和Cbd的阻抗值增加，相对于这些阻抗来说，串联电阻变得不重要了，故可忽略。还有，随着频率的降低，电感的阻抗减小，因而与和它串联的电阻相比，这一元件可以略去。最后，在低频时，电流源分母的值近似等于1。MOS管非准静态模型的复指数激励。可见，这种情况下，图9.19中的模型就简化为图8.13的模型。

这里的模型也可与9.2节中的完整准静态模型联系起来。低频时，图9.19中串联的RC组合，由于上面已经讨论的原因，简化成图9.5中相应的电容。此外，如果假设ωτ₁《1，则就可使用近似式1／(1+jωτ₁)≈1-jωτ₁，  因而可把式(9.4.69f)至(9.4.69h)写成如下形式：

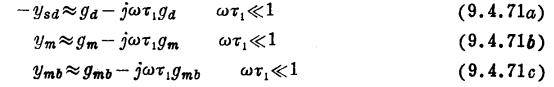
把式(9.4.71)与完整准静态模型的-sd、m和mb[式(9.3.11f)至(9.3.11h)]相比较表明，两者的形式是一样的(回想一下Csd是一负值)。进一步检查这些方程中的各个参数的表达式发现，事实上式(9.4.71)至(9.4.71c)不仅在形式上，而且在元件值上都和式(9.3.11f)至(9.3.11h)完全相同。因此，假设Cmx可以忽略，  图9.19中的模型便简化为图9.5中的完整准静态模型。特别注意，图9.19中电阻-电感的串联组合简化为电阻和负电容的并联组合。随着频率进一步降低，-sd、m和mb中含ω的项可以忽略，从而使模型简化为图8.13中的简化模型。

图9.19中的受控电源的系数是复数，这可能使这一模型不能直接用于一些计算机分析程序。采用下面这样的写法可以避免发生这个问题：

其中

把式(9.4.71)与完整准静态模型的-sd、m和mb[式(9.3.11f)至(9.3.11h)]相比较表明，两者的形式是一样的(回想一下Csd是一负值)。进一步检查这些方程中的各个参数的表达式发现，事实上式(9.4.71)至(9.4.71c)不仅在形式上，而且在元件值上都和式(9.3.11f)至(9.3.11h)完全相同。因此，假设Cmx可以忽略，  图9.19中的模型便简化为图9.5中的完整准静态模型。特别注意，图9.19中电阻-电感的串联组合简化为电阻和负电容的并联组合。MOS管非准静态模型的复指数激励。随着频率进一步降低，-sd、m和mb中含ω的项可以忽略，从而使模型简化为图8.13中的简化模型。

图9.19中的受控电源的系数是负数，这可能使这一模型不能直接用于一些计算机分析程序。采用下面这样的写法可以避免发生这个问题：

其中

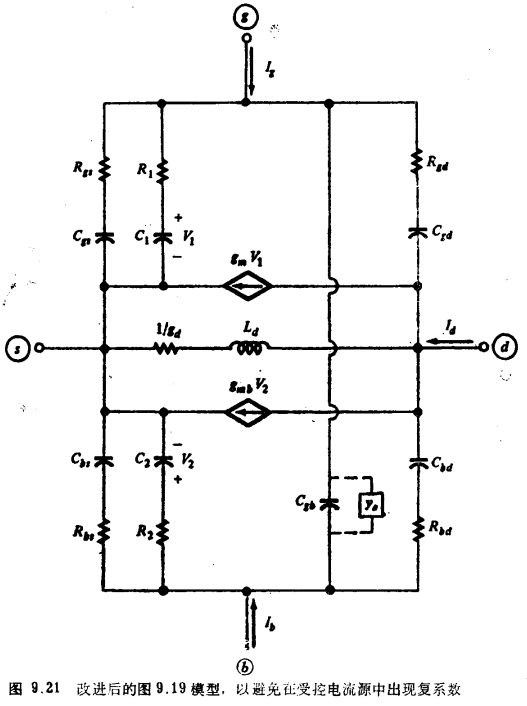
   利用两个简单电路很容易从Vgs得到V1，从Vbs得到V2。图9.21利用了这个思想，  只要R1C1=τ1和R2C2=τ1，不难证明对于该图，式(9.4.73)成立。  但是，为了不破坏这个模型，我们必须保证新加元件中的电流可以忽略(与只Rgs-Cgs和Rbs-Cbs支路中的电流相比)。例如通过选用，下列元件值便可保证实现这一点：

在饱和区，图9.21的模型呈简单形式，如图9.22所示，这一形式不难从上述关系式推导出来、在饱和区，g_d模拟沟道长度调制效应。对低频时的这一效应已经有过大量的研究，但在本节模型的推导中未曾把它包括进去。因此，没有理由假设如式(9.4.70c)那样给定的Ld用于饱和区时会是正确的，在实际中，这可能不是一个问题i因为在电路中，源和漏之间总有电容存在(例如，有另外一个晶体管连向讨论中的晶体管，或者有寄生电容)。在Ld的阻抗变得可与1/g_d和L_d的微小的小信号电流也许可以忽略。

联系方式：邹先生

联系电话：0755-83888366-8022

手机：18123972950

QQ：2880195519

联系地址：深圳市福田区车公庙天安数码城天吉大厦CD座5C1

请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号

请“关注”官方微信公众号:提供  MOS管  技术帮助