解析与衬底同型的注入强反型漏端电流模型对于图6.10所示的连接方式,非饱和区的漏端电流可以据根式(4.4.13)确定,现将该式重写于下: 暂且假定μ为常数。[迁移率对栅电场的依赖性可以用有效迁移率方法来考虑(4.8节)。根据这个假定,并利用式(6.2.21)的Q´I,式(6.2.24)变成 假设VDBVSB(VDS0),我们分三种情况来说明漏端电流:1、VSB VDB≤VI。如果忽略十
解析与衬底同型的注入强反型漏端电流模型对于图6.10所示的连接方式,非饱和区的漏端电流可以据根式(4.4.13)确定,现将该式重写于下: 暂且假定μ为常数。[迁移率对栅电场的依赖性可以用有效迁移率方法来考虑(4.8节)。根据这个假定,并利用式(6.2.21)的Q´I,式(6.2.24)变成 假设VDBVSB(VDS0),我们分三种情况来说明漏端电流:1、VSB VDB≤VI。如果忽略十

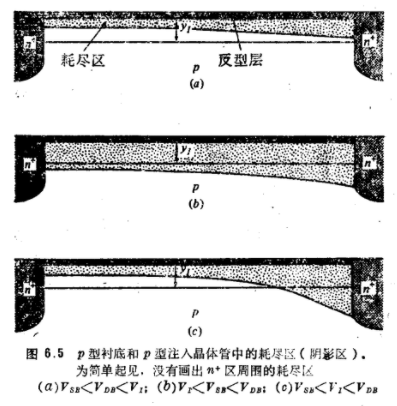
与衬底同型的注入MOS晶体管电荷和阈值电压本节讨论图6.10a中的具有p型衬底和p型注入的晶体管。我们的目标是导出一个漏端电流的简单模型,该模型能近似地预计实测I-V特性的一些重要性质。我们将把注入浓度的分布形状假设为如图6.2b所示的矩形。电荷和阈值电压首先考虑图6.1b的对应的三端结构,并假设VCB很小。随着VGB的增加,在表面形成耗尽区。耗尽区的宽度随VGB的增加而增大,直到建立起强反型层,
与衬底同型的注入MOS晶体管电荷和阈值电压本节讨论图6.10a中的具有p型衬底和p型注入的晶体管。我们的目标是导出一个漏端电流的简单模型,该模型能近似地预计实测I-V特性的一些重要性质。我们将把注入浓度的分布形状假设为如图6.2b所示的矩形。电荷和阈值电压首先考虑图6.1b的对应的三端结构,并假设VCB很小。随着VGB的增加,在表面形成耗尽区。耗尽区的宽度随VGB的增加而增大,直到建立起强反型层,

离子注入沟道MOS晶体管的三端结构作用特性 迄今为止,对所讨论的晶体管都假设它们具有均匀掺杂的衬底。对于非离子注入沟道器件而言,这一假设是合理的(虽然严格地说并不正确,因为在氧化层生长过程中杂质会重新分布)。本章将讨论这样一类器件,即通过离子注入有意识地使源漏之间的衬底掺杂很不均匀,所谓离子注入就是在制造过程中用离子轰击衬底。这些离子到达之处,也就是衬底有效浓度改变之地。离子注入也可用于给硅
离子注入沟道MOS晶体管的三端结构作用特性 迄今为止,对所讨论的晶体管都假设它们具有均匀掺杂的衬底。对于非离子注入沟道器件而言,这一假设是合理的(虽然严格地说并不正确,因为在氧化层生长过程中杂质会重新分布)。本章将讨论这样一类器件,即通过离子注入有意识地使源漏之间的衬底掺杂很不均匀,所谓离子注入就是在制造过程中用离子轰击衬底。这些离子到达之处,也就是衬底有效浓度改变之地。离子注入也可用于给硅

MOS晶体管按比例缩小(Scaling)作用特性解析为了提高速度和单位面积芯片上电路的集成度,需要作些努力使晶体管做得尽可能小。然而,如果沟道长度做得太小,源和漏周围的耗尽区有可能连成一片,从而可能出现5.6节中讨论过的穿通现象。因此,为了把L做小,就应使耗尽区的宽度也变小。这一点可用增加衬底掺杂浓度和降低反偏电压来实现。为了在任意电路工作条件下都能实现降低反偏电压,就必须降低电源电压。增加掺杂浓
MOS晶体管按比例缩小(Scaling)作用特性解析为了提高速度和单位面积芯片上电路的集成度,需要作些努力使晶体管做得尽可能小。然而,如果沟道长度做得太小,源和漏周围的耗尽区有可能连成一片,从而可能出现5.6节中讨论过的穿通现象。因此,为了把L做小,就应使耗尽区的宽度也变小。这一点可用增加衬底掺杂浓度和降低反偏电压来实现。为了在任意电路工作条件下都能实现降低反偏电压,就必须降低电源电压。增加掺杂浓

MOS晶体管源区的和漏区的串联电阻效应MOS品体管的沟道与两个“寄生”电阻互相串联,一个与源区有关,另一个与漏区有关[118117]。每个电阻都可认为由三部分组成:(1)金属与n*区的接触电阻;(2)n*区的主体电阻;(3)当电流从n*区流向通常较薄的反型层时,与电流流动路线的聚集有关的电阻(“扩展电阻”效应[4ls1l])。用R表示由于这些效应产生的与沟道两末端之一串联的总电阻,于是就得到
MOS晶体管源区的和漏区的串联电阻效应MOS品体管的沟道与两个“寄生”电阻互相串联,一个与源区有关,另一个与漏区有关[118117]。每个电阻都可认为由三部分组成:(1)金属与n*区的接触电阻;(2)n*区的主体电阻;(3)当电流从n*区流向通常较薄的反型层时,与电流流动路线的聚集有关的电阻(“扩展电阻”效应[4ls1l])。用R表示由于这些效应产生的与沟道两末端之一串联的总电阻,于是就得到

MOS晶体管穿通,击穿,寄生电流和有关效应本节中我们将讨论一些干扰“正常“MO3品体管特性的不良现象大部分这些现象可用二维计算机模拟来预测,但是未能使它们成为解祈模型。由于这些效应能够通过合理的器件设计(第10章)和避免应用在特大的偏置电压下而加以消除,故这里只作很简单的讨论。在讨论中,除非另有说明,通常假定器件是n沟的。
MOS晶体管穿通,击穿,寄生电流和有关效应本节中我们将讨论一些干扰“正常“MO3品体管特性的不良现象大部分这些现象可用二维计算机模拟来预测,但是未能使它们成为解祈模型。由于这些效应能够通过合理的器件设计(第10章)和避免应用在特大的偏置电压下而加以消除,故这里只作很简单的讨论。在讨论中,除非另有说明,通常假定器件是n沟的。
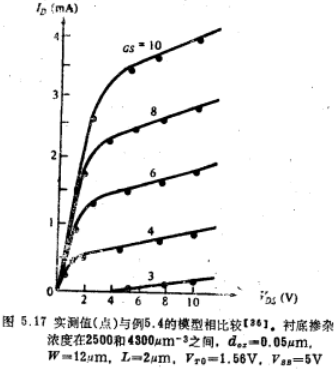
MOS晶体管组合几种效应于一个模型之中迄今今我们已经讨论了各种效应,为简单起见,每次只考虑一种。但是,在一个实际的器件模型中,必须同时考虑若干个这种效应。为了恰当地做到这一点,必须研究这些效应之间的相互作用,但遗憾的是,这样所得的表达式将变得十分复杂。如果每种效应独自的影响较小,则经常采用的一种经验方法是假设这些效应之间无相互作用。举例来说,考虑一个沟道底短又窄的器件。为了获得正确结果,这里需要用
MOS晶体管组合几种效应于一个模型之中迄今今我们已经讨论了各种效应,为简单起见,每次只考虑一种。但是,在一个实际的器件模型中,必须同时考虑若干个这种效应。为了恰当地做到这一点,必须研究这些效应之间的相互作用,但遗憾的是,这样所得的表达式将变得十分复杂。如果每种效应独自的影响较小,则经常采用的一种经验方法是假设这些效应之间无相互作用。举例来说,考虑一个沟道底短又窄的器件。为了获得正确结果,这里需要用

MOS短沟道器件势全下降-二维电荷共享和阈值电压总结和评论我们已经看到,有几种因素会影响有效阀值电压的值。根据长沟道器件的一般表达式,以及上述关于小沟道的讨论,我们可以定性地总结出以下几条;有效阀值电压将会增加,当:1.衬底掺杂浓度增加。2.氧化层厚度增加。3.沟道长度增加。4.沟道宽度减小。5.结深减小。有效岗值电压的概念代表我们为了使一些众所周知的公式(针对长沟道和宽沟道器件所导出的)在原则上
MOS短沟道器件势全下降-二维电荷共享和阈值电压总结和评论我们已经看到,有几种因素会影响有效阀值电压的值。根据长沟道器件的一般表达式,以及上述关于小沟道的讨论,我们可以定性地总结出以下几条;有效阀值电压将会增加,当:1.衬底掺杂浓度增加。2.氧化层厚度增加。3.沟道长度增加。4.沟道宽度减小。5.结深减小。有效岗值电压的概念代表我们为了使一些众所周知的公式(针对长沟道和宽沟道器件所导出的)在原则上

MOS晶体管窄沟道器件一个器件沿其沟道宽度方向的截面示于图5-13。为简单起见,此图画得非常理想化。个实际器件的沟道截面因某些制造工艺看上去可能如图5.13b。一层厚氧化物渐渐地变薄,形成了如图所示的被称为“鸟咀”(第10章)的特征形状。从两幅图中都可看出,耗尽区并不正好限于薄氧化层下面的区域内。这是因为从栅电荷出发的场强线有一些终止在沟道两侧的电离受主上。这些场强线构成了所谓边缘场。如果W较大
MOS晶体管窄沟道器件一个器件沿其沟道宽度方向的截面示于图5-13。为简单起见,此图画得非常理想化。个实际器件的沟道截面因某些制造工艺看上去可能如图5.13b。一层厚氧化物渐渐地变薄,形成了如图所示的被称为“鸟咀”(第10章)的特征形状。从两幅图中都可看出,耗尽区并不正好限于薄氧化层下面的区域内。这是因为从栅电荷出发的场强线有一些终止在沟道两侧的电离受主上。这些场强线构成了所谓边缘场。如果W较大

MOS管漏源电压的影响及其阈值电压分析上面的一些结果是在VDS小到可以忽略的条件下导出来的。当VSB固定时,如果VDS(因而也是VDB)增加,则漏区周围的耗尽区将变宽。按照前面的论点可知,这又将使值减少,小于迄今所求得的值,从而使T进一步减小。这样,对于短沟道器件来说,T成了VDS的降函数!有效电荷仍可用类似于图5.9a的方法进行计算,只是此刻图中的梯形畸变了。最终所得的表达式将在题5.15中考虑
MOS管漏源电压的影响及其阈值电压分析上面的一些结果是在VDS小到可以忽略的条件下导出来的。当VSB固定时,如果VDS(因而也是VDB)增加,则漏区周围的耗尽区将变宽。按照前面的论点可知,这又将使值减少,小于迄今所求得的值,从而使T进一步减小。这样,对于短沟道器件来说,T成了VDS的降函数!有效电荷仍可用类似于图5.9a的方法进行计算,只是此刻图中的梯形畸变了。最终所得的表达式将在题5.15中考虑