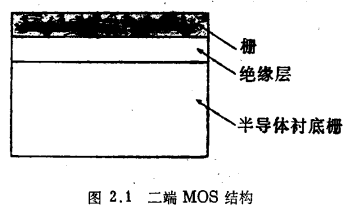
二端 MOS结构基础作用及其特性分析二端 MOS结构在由简单的MOS结构向完整的MOS晶体管逐步推导的过程中,本章先考虑二端 MOS结构。这种结构常称为“MOS电容”,示于图2.1。制造这种结构,应先准备p型或n型半导体材料,这种材料称为衬底或本体,并从现在起假设是硅,通常掺杂浓度是102至104μm-3(第6章前只考虑均匀掺杂的衬底)。先在衬底上面生成一层绝缘物,通常为二氧化硅(SiO2),简称
二端 MOS结构基础作用及其特性分析二端 MOS结构在由简单的MOS结构向完整的MOS晶体管逐步推导的过程中,本章先考虑二端 MOS结构。这种结构常称为“MOS电容”,示于图2.1。制造这种结构,应先准备p型或n型半导体材料,这种材料称为衬底或本体,并从现在起假设是硅,通常掺杂浓度是102至104μm-3(第6章前只考虑均匀掺杂的衬底)。先在衬底上面生成一层绝缘物,通常为二氧化硅(SiO2),简称

PN结器件的电流-电压特性及其小信号等效电路PN结器件对硅材料的一个区城用型杂质,对相邻区域用p型杂质作选择掺杂可制成一个所谓pn结,这样一个结示于图1.15中。在这图中,我们假设在从n型到p型的边界上,掺杂类型突然改变,且边界两边的掺杂浓度都是均匀的,这样一种结称为突变结或阶跃结。在画图1.15时,我们也已假定n区的掺杂重于p型区。顶部和底部的帽子由选定的金属制成,以实现与半导体的“欧姆接触”(
PN结器件的电流-电压特性及其小信号等效电路PN结器件对硅材料的一个区城用型杂质,对相邻区域用p型杂质作选择掺杂可制成一个所谓pn结,这样一个结示于图1.15中。在这图中,我们假设在从n型到p型的边界上,掺杂类型突然改变,且边界两边的掺杂浓度都是均匀的,这样一种结称为突变结或阶跃结。在画图1.15时,我们也已假定n区的掺杂重于p型区。顶部和底部的帽子由选定的金属制成,以实现与半导体的“欧姆接触”(

接触电器几种材料串联中的作用及其结构接触电器几种材料串联现在我们可以来进行一项有意义的观察,即考虑几种材料的串联,如图1.14α所示,如前所述,所有材料都处于同一温度。如果我们把电势差ψKL用这串联结构中的各接触电势来表示,则有然后在上式中重复运用式(1.4.4),可得:显然,在和式中,除ΦJ1和ΦJn以外,每个ΦJi都出现两次,一次为加,一次为减,因此有① 在能得处现方法中,接施电势常用两种材料
接触电器几种材料串联中的作用及其结构接触电器几种材料串联现在我们可以来进行一项有意义的观察,即考虑几种材料的串联,如图1.14α所示,如前所述,所有材料都处于同一温度。如果我们把电势差ψKL用这串联结构中的各接触电势来表示,则有然后在上式中重复运用式(1.4.4),可得:显然,在和式中,除ΦJ1和ΦJn以外,每个ΦJi都出现两次,一次为加,一次为减,因此有① 在能得处现方法中,接施电势常用两种材料

半导体器件物理接触电势差与什么有关详细谈论接触电势现在来考虑由两种不同材料J1和J2形成的、无外加偏压的一个结,如图1.9a所示。每一种材料都可以是半导体或金属。当两种材料放在一起时,由于J1和J2中载流子的能量一般说来是不相同的,而且在原先为中性的材料内部,不存在相反方向的电场,所以一开始载流子将从一种材料流向另一种材料。然而,随着每个带电载流子穿过这个结,在它后面便留下了一个相反极性的净电荷,
半导体器件物理接触电势差与什么有关详细谈论接触电势现在来考虑由两种不同材料J1和J2形成的、无外加偏压的一个结,如图1.9a所示。每一种材料都可以是半导体或金属。当两种材料放在一起时,由于J1和J2中载流子的能量一般说来是不相同的,而且在原先为中性的材料内部,不存在相反方向的电场,所以一开始载流子将从一种材料流向另一种材料。然而,随着每个带电载流子穿过这个结,在它后面便留下了一个相反极性的净电荷,

半导体扩散工艺基础技术原理概述分析漂移仅仅是半导体中形成电流的两种机制之一。另一种机制是扩散,它发生在当粒子的空间分布不均匀时,即存在“浓度梯度”时,粒子的随机运动促使它们从浓度高处向浓度低处扩散。注意,这种现象不是由电场引起的,因此与粒子是否带电无关。例如烟雾粒子就显示出这种扩散现象。然而,如果这些粒子带了电,如电子和空穴,则扩散引起了电荷的运动,因而产生了电流。让我们借助于图1.8α来考虑扩散
半导体扩散工艺基础技术原理概述分析漂移仅仅是半导体中形成电流的两种机制之一。另一种机制是扩散,它发生在当粒子的空间分布不均匀时,即存在“浓度梯度”时,粒子的随机运动促使它们从浓度高处向浓度低处扩散。注意,这种现象不是由电场引起的,因此与粒子是否带电无关。例如烟雾粒子就显示出这种扩散现象。然而,如果这些粒子带了电,如电子和空穴,则扩散引起了电荷的运动,因而产生了电流。让我们借助于图1.8α来考虑扩散
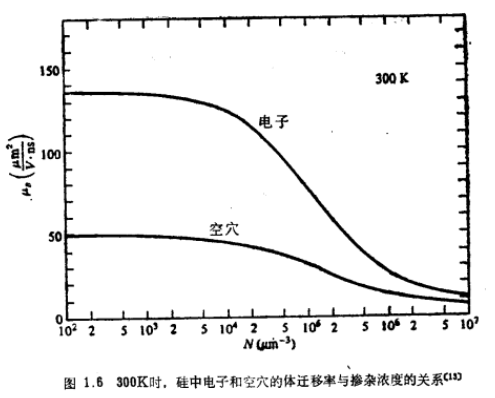
弱电场情况上述这些关系式在弱电场情况下变成特别有用的形式。对于硅,粗略地说,“弱”电场意味着对电子来说小于0.3V/μm;对空穴来说小于0.6V/μm。在这种电场下,▏υd▕正比于▏▕,如图1.4曲线的底段那样,这比例常数称为迁移率,用μB表示。下标B用来强调这一迁移率是指半导体的“体”特性。读者必须把它和第4章中将介绍的“表面”迁移率加以区别。于是我们有在室温下,硅的电子和空穴的迁移率与掺杂浓度
弱电场情况上述这些关系式在弱电场情况下变成特别有用的形式。对于硅,粗略地说,“弱”电场意味着对电子来说小于0.3V/μm;对空穴来说小于0.6V/μm。在这种电场下,▏υd▕正比于▏▕,如图1.4曲线的底段那样,这比例常数称为迁移率,用μB表示。下标B用来强调这一迁移率是指半导体的“体”特性。读者必须把它和第4章中将介绍的“表面”迁移率加以区别。于是我们有在室温下,硅的电子和空穴的迁移率与掺杂浓度
半导体漂移与电场强度的关系分析漂移现在让我们考虑一段没有外加电场的半导体,空穴和电子在所有方向上都有随机的“热”运动。然而,平均地看来,这些电荷的随机运动互相抵消,因此不会产生净电流。如果加上电场(例如把这段半导体的两端连上一个电池),则该电场将施加作用力于带电粒子。于是沿着场强线方向将有一个净运动,这种定向运动在宏观上被观察为电流。这一现象称为漂移;如果粒子未带电,那么漂移是不会发生的。在漂移过
半导体漂移与电场强度的关系分析漂移现在让我们考虑一段没有外加电场的半导体,空穴和电子在所有方向上都有随机的“热”运动。然而,平均地看来,这些电荷的随机运动互相抵消,因此不会产生净电流。如果加上电场(例如把这段半导体的两端连上一个电池),则该电场将施加作用力于带电粒子。于是沿着场强线方向将有一个净运动,这种定向运动在宏观上被观察为电流。这一现象称为漂移;如果粒子未带电,那么漂移是不会发生的。在漂移过
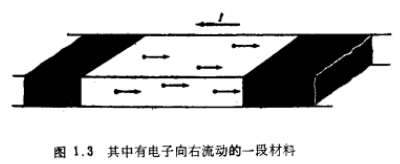
半导体器件-渡越时间的定义和材料分析渡越时间“渡越时间”这一概念将用于后续章节中对MOS晶体管的讨论,这个概念是通用的,并且与产生电流导通的一些机制无关。因此在讨论这些机制以前,首先引入这个概念。请看图1.3中两个阴影区域之间的一段材料。假设其中完全由于自由电子的流动已经建立起沿一个方向的稳定电流,还假设没有电子与空穴的复合过程。电子源源不断地从左边供给,并以同一固定的速率从右边流出。于是,在任意
半导体器件-渡越时间的定义和材料分析渡越时间“渡越时间”这一概念将用于后续章节中对MOS晶体管的讨论,这个概念是通用的,并且与产生电流导通的一些机制无关。因此在讨论这些机制以前,首先引入这个概念。请看图1.3中两个阴影区域之间的一段材料。假设其中完全由于自由电子的流动已经建立起沿一个方向的稳定电流,还假设没有电子与空穴的复合过程。电子源源不断地从左边供给,并以同一固定的速率从右边流出。于是,在任意

半导体这个名称起因于这一事实:它们在传导电流方面优于绝缘体,但不如导体。目前最广泛使用的半导体材料是硅,所以下面的讨论集中在这一材料上,但是这里所用的一些定性的论点对于别的半导体材料也适用。全书中,假定不存在光照、辐射、机械应力和磁场,以及半导体各点上的温度相同(除指明外,这一温度应理解为室温)。在未作进一步说明前,我们还假定所讨论的半导体材料是没有外加电压或电流的独立体,并且它周围的
半导体这个名称起因于这一事实:它们在传导电流方面优于绝缘体,但不如导体。目前最广泛使用的半导体材料是硅,所以下面的讨论集中在这一材料上,但是这里所用的一些定性的论点对于别的半导体材料也适用。全书中,假定不存在光照、辐射、机械应力和磁场,以及半导体各点上的温度相同(除指明外,这一温度应理解为室温)。在未作进一步说明前,我们还假定所讨论的半导体材料是没有外加电压或电流的独立体,并且它周围的

高速低温CMOS电路性能及其温度变化解析高速低温CMOS电路性能CMOS电路的抗闩锁(Latch-up)性能也与温度密切相关。Latch-up的产生是由于杂散npn和pmp双极管之间的正反馈所致。当温度降低时这些双极管的电流增益β会大大降低。以垂直杂散双极管为例,在室温下β=230,降至液氮温度77K时β减至为4,在4.2K下β为0.4。因此,在低温下工作的CMOS集成电路几乎不存在Latch-u
高速低温CMOS电路性能及其温度变化解析高速低温CMOS电路性能CMOS电路的抗闩锁(Latch-up)性能也与温度密切相关。Latch-up的产生是由于杂散npn和pmp双极管之间的正反馈所致。当温度降低时这些双极管的电流增益β会大大降低。以垂直杂散双极管为例,在室温下β=230,降至液氮温度77K时β减至为4,在4.2K下β为0.4。因此,在低温下工作的CMOS集成电路几乎不存在Latch-u