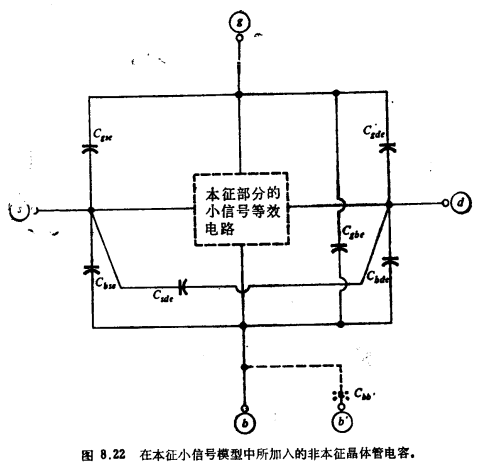
MOS晶体管非本征部分的小信号的栅重迭电容解析晶体管的“非本征”部分是指图8.21a虚线以外的所有部分。在图8.21a及顶图8.21b中，我们给出了在下面讨论中要用到的一些符合的定义。与非本征部分有关的电荷存储效应可用6个小信号电容来模拟（每一对端子之间有一个电容，如图8.22所示）在用于这些电容的符号中，前两个下标指明有关的器件端，下标c代表非本征的。MOS晶体管非本征部分的小信号。若晶体管恰巧
MOS晶体管非本征部分的小信号的栅重迭电容解析晶体管的“非本征”部分是指图8.21a虚线以外的所有部分。在图8.21a及顶图8.21b中，我们给出了在下面讨论中要用到的一些符合的定义。与非本征部分有关的电荷存储效应可用6个小信号电容来模拟（每一对端子之间有一个电容，如图8.22所示）在用于这些电容的符号中，前两个下标指明有关的器件端，下标c代表非本征的。MOS晶体管非本征部分的小信号。若晶体管恰巧
MOS晶体管通用电荷薄层模型作用及其重要特征7.4.5节中，我们已经说明怎样用4.3节中的通用模型来计算各种电荷。最后得到的表达式适用于所有反型区。对这些电荷求导可得电容（这不是一件容易的事）。除非对本体电荷采用采用近似式(类似于4.4节中导出近似强反型时所用的近似式)否则最后得到的表达式太长。为了说明在所有反型区中电容的变化情况，可以固定VDS， 画出电容与VGS的关系曲线。这就是在画图7.9
MOS晶体管通用电荷薄层模型作用及其重要特征7.4.5节中，我们已经说明怎样用4.3节中的通用模型来计算各种电荷。最后得到的表达式适用于所有反型区。对这些电荷求导可得电容（这不是一件容易的事）。除非对本体电荷采用采用近似式(类似于4.4节中导出近似强反型时所用的近似式)否则最后得到的表达式太长。为了说明在所有反型区中电容的变化情况，可以固定VDS， 画出电容与VGS的关系曲线。这就是在画图7.9
本征截止频率：考虑连接为如图8．16a所示的一个晶体管，假设其中的偏置电压使得管子工作在饱和区。电压源正QiⅡ06是角频率为O(1ad／6)的一个正弦小信号。对于这种连接的小信号等效电路可以用图8．13的电路取代晶体管，并用短路线取代所有的直流电压源(由于这些电压源的刀r二0)而导出来。现在，移去与短路线并联的所有元件，并注意饱和时，Ogd为零，就可得到冈8．16b的电路。小信号漏端电流和栅电流可
本征截止频率：考虑连接为如图8．16a所示的一个晶体管，假设其中的偏置电压使得管子工作在饱和区。电压源正QiⅡ06是角频率为O(1ad／6)的一个正弦小信号。对于这种连接的小信号等效电路可以用图8．13的电路取代晶体管，并用短路线取代所有的直流电压源(由于这些电压源的刀r二0)而导出来。现在，移去与短路线并联的所有元件，并注意饱和时，Ogd为零，就可得到冈8．16b的电路。小信号漏端电流和栅电流可
解析MOS晶体管本征部分的中频小信号的强反型原理强反型区的精确电容表达式可利用上面的电容定义，并结合对应于4.4.1节中的精确模型的电荷表达式推导出来。这些电荷表达式在附录L中给出。可是，导出的电容表达式是复杂的。为了简单一些，可利用对应于、4.4.2节中的近似模型的电荷表达式来推导近似的电容表达式。事实上，使用中的大多数电容模型是从这些电荷表达式导出来的，这些电荷表达假设了单位面积耗尽区电荷Q´
解析MOS晶体管本征部分的中频小信号的强反型原理强反型区的精确电容表达式可利用上面的电容定义，并结合对应于4.4.1节中的精确模型的电荷表达式推导出来。这些电荷表达式在附录L中给出。可是，导出的电容表达式是复杂的。为了简单一些，可利用对应于、4.4.2节中的近似模型的电荷表达式来推导近似的电容表达式。事实上，使用中的大多数电容模型是从这些电荷表达式导出来的，这些电荷表达假设了单位面积耗尽区电荷Q´
MOS晶体管本征部分的中频小信号等效电路解析当施于MOS晶体管的小信号电压快速变化时，小信号端电流会大大地不同于图8.2电路所预测的电流。现在我们采介绍一种简单模型，该模型可预测这时的电流特性，只要小信号电压的频率不是太高。MOS晶体管本征部分的中频小信号。通过假设准静态工作，并考虑到电荷存储效应，可使该模型实现这一点。并非所有电荷存储效应都包括在这一模型中；另外的一些电荷存储效应将在第9章中考虑
MOS晶体管本征部分的中频小信号等效电路解析当施于MOS晶体管的小信号电压快速变化时，小信号端电流会大大地不同于图8.2电路所预测的电流。现在我们采介绍一种简单模型，该模型可预测这时的电流特性，只要小信号电压的频率不是太高。MOS晶体管本征部分的中频小信号。通过假设准静态工作，并考虑到电荷存储效应，可使该模型实现这一点。并非所有电荷存储效应都包括在这一模型中；另外的一些电荷存储效应将在第9章中考虑
MOS管晶体管低频小信号的通用模型重要性在4.3节中已说明，对于长沟道器件(忽略沟道长度调制效应)可导出适用于所有工作区的一般表达式[式(4.3.8)，(4.3.16)和(4.3.17)]。这样一类表达式可用来提供小信号电导的表达式，该表达式将适用于包括中反型在内的所有工作区和强反型时从非饱和到饱和的过渡区。当然，这里的困难将是公式的复杂性。式(4.3.16)的漏端电流公式中显式地包含了VGB，通
MOS管晶体管低频小信号的通用模型重要性在4.3节中已说明，对于长沟道器件(忽略沟道长度调制效应)可导出适用于所有工作区的一般表达式[式(4.3.8)，(4.3.16)和(4.3.17)]。这样一类表达式可用来提供小信号电导的表达式，该表达式将适用于包括中反型在内的所有工作区和强反型时从非饱和到饱和的过渡区。当然，这里的困难将是公式的复杂性。式(4.3.16)的漏端电流公式中显式地包含了VGB，通
MOS晶体管低频小信号中反型工作原理及其特性在4.5节中已注意到，许多ID模型中忽略了中反型区，从而认为弱反型区和强反型区是紧挨的。这在预测ID时会导致某种误差，这一误差对若干应用来说是可以接受的。但是遗憾的是，在小信号参数中引起的相应误差通常是不可接受的，而且不论对模型参数选择什么样的经验值都不能使它减小。为举例说明这一点，我们选择gm作为例子， 并考虑VDS固定，VGS在较大范围内变化时这一
MOS晶体管低频小信号中反型工作原理及其特性在4.5节中已注意到，许多ID模型中忽略了中反型区，从而认为弱反型区和强反型区是紧挨的。这在预测ID时会导致某种误差，这一误差对若干应用来说是可以接受的。但是遗憾的是，在小信号参数中引起的相应误差通常是不可接受的，而且不论对模型参数选择什么样的经验值都不能使它减小。为举例说明这一点，我们选择gm作为例子， 并考虑VDS固定，VGS在较大范围内变化时这一
MOS晶体管低频小信号模型弱反型的原理及电流定义MOS晶体管低频小信号模型弱反型把弱反型电流公式(4.6.17)代入gm的定义式(8.2.1)，求得其中n由式(4.6.20)给出，且假定界面陷阱效应可忽略，对于许多现代器件，这是一个有效的假设(2.6节)。如果这一效应不可忽略，则n的值会更大，且最好用实验来确定。这样，与强反型时的特性相反，值gm/ID与W／L无关，这是由于弱反型时，ID是VGS的
MOS晶体管低频小信号模型弱反型的原理及电流定义MOS晶体管低频小信号模型弱反型把弱反型电流公式(4.6.17)代入gm的定义式(8.2.1)，求得其中n由式(4.6.20)给出，且假定界面陷阱效应可忽略，对于许多现代器件，这是一个有效的假设(2.6节)。如果这一效应不可忽略，则n的值会更大，且最好用实验来确定。这样，与强反型时的特性相反，值gm/ID与W／L无关，这是由于弱反型时，ID是VGS的
MOS晶体管低频小信号模型强反型的原理及关系曲线栅跨导考虑一个具有恒定有效迁移率的长沟道器件。把4.4节中的精确或近似模型用于gm的定义式中，可求得利用定义于式(4.4.31)中的参数α，上式可简明地表示如下：在饱和区，近似模型式(4.4.30b)给出电流，此式与式(8.2.1)一起可导出gm的下列等效形式：从式（8.2.6α）可看到，在非饱和区，gm与VGS无关，这一点明鲜地表示在图8.3中，我
MOS晶体管低频小信号模型强反型的原理及关系曲线栅跨导考虑一个具有恒定有效迁移率的长沟道器件。把4.4节中的精确或近似模型用于gm的定义式中，可求得利用定义于式(4.4.31)中的参数α，上式可简明地表示如下：在饱和区，近似模型式(4.4.30b)给出电流，此式与式(8.2.1)一起可导出gm的下列等效形式：从式（8.2.6α）可看到，在非饱和区，gm与VGS无关，这一点明鲜地表示在图8.3中，我
解析MOS晶体管低频小信号模型定义和等效电路前一章考虑了端电压随时间变化的MOS晶体管。但对这些电压变化量的大小未加任何限制。本章将考虑这样一种情况；端电压变化足够小，使所引起的微小电流变化与电压变化的关系可用线性关系式来表示。我们将要推导这样一些线性关系式，并研究用线性电路来表示它们。这些电路称为小信号等效电路。当这些电路的激励电压等于实际端电压的小变化量时，这些电路中产生的电流将等于实际晶体管
解析MOS晶体管低频小信号模型定义和等效电路前一章考虑了端电压随时间变化的MOS晶体管。但对这些电压变化量的大小未加任何限制。本章将考虑这样一种情况；端电压变化足够小，使所引起的微小电流变化与电压变化的关系可用线性关系式来表示。我们将要推导这样一些线性关系式，并研究用线性电路来表示它们。这些电路称为小信号等效电路。当这些电路的激励电压等于实际端电压的小变化量时，这些电路中产生的电流将等于实际晶体管
深圳市龙华区大浪街道浪口社区英泰路8号英泰科汇广场2栋1902
KIA-公众号
Copyright ©2015 广东可易亚半导体科技有限公司
深圳市龙华区大浪街道浪口社区英泰路8号英泰科汇广场2栋1902
KIA-公众号
