电子技术论坛
信息来源: 时间:2022-9-16
MOS信号模拟、数字和抽样-模拟信号和系统
变换方法
开关电容滤波器是以模拟信号表示的抽样数据电路。因此,一般来说它们的分析既需要模拟信号的数学工具(拉普拉斯和傅里叶变换),又需要抽样信号的数学工具(Z变换)。而且,这两类变换间的关系必须正确地给以阐述和使用。为此,本章概要地给出模拟,数字和抽样一模拟系统的基本定义,然后讨论分析它们在时域和频域响应时需要的各种变换方法。最后,将描述从适当的模拟“原型”系统获得抽样数据系统传递函数的设计技术。
模拟、数字和抽样-模拟信号和系统
一个信号就是一个函数:在我们的应用中,函数的自变量是时间,因变量是一个如电压、电流或电荷的物理量。连续时间信号是一个在所讨论的时间区间内处处有确定值的信号(图2.1(a))。离散时间信号仅在离散的时间点(通常是等步长分隔)有值(图2.1(b)),而在其它任何时间上没有给予表示。离散时间信号,常常通过对一个连续时间信号抽样得到。因此,图2.1(b)所示的信号与图2.1(a)的信号满足下列关系式
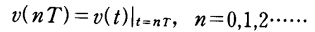
这里,T是抽样间隔。另一类密切相关的信号是图2.1(c)中表示的抽样一保持信号。它满足
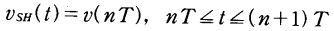
因此,抽样一保持信号(S/H)是一种仅在离散时间瞬刻变化量值连续时间信号。它完全由T和υ(nT),n=0,1,2,……的值确定。
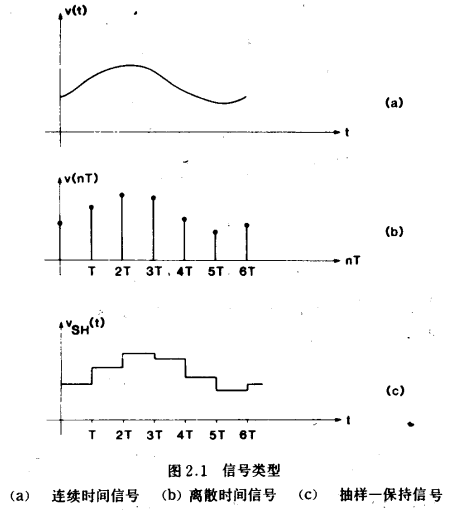
数字信号是一个数字序列。每一个数表示离散时间信号的某一量值υ(nT)。然而,数字信号中的数仅能用一个有限位的数字(如果信号是二进制码,即为比特)表示。因此,它们只能取离散值,这些值是最小有效数字的整倍数。相反,函数υ(t)、υ(nT)和lυSH(t)可以取任何量值,被称为模拟信号。后两类函数,υ(nT)和υSH(t)也常常称为抽样-模拟信号或抽样-数据模拟信号。
系统是能够处理信号的物理装置。根据它能处理的信号的类型而被称为模拟的或数字的、连续的或离散的系统等等。数字计算机是数字系统的一个例子,放大器则是连续时间模拟系统的一个例子。在本书中讨论的大部分电路处理的是如图2.1(c)所示的抽样一保持模拟信号。因此它们是一种特殊类型的连续时间模拟系统,用来变换输入S/H信号为另一个输出S/H信号。
处理电压、电流、磁通和电荷等电信号的模拟系统便是电路或网络。电路分析是通过建立网络方程和解网络方程来完成的。这些方程一般是通过下列三种关系获得的:基尔霍夫电压定律(KVZ)即电路中任何闭合回路上电压之和为零;基尔霍夫电流定律(KCL)即进入任何节点的电流之和为零;网络中的具体电路元件(电阻器、电容器、放大器等)确定的支路关系。
KVL和KCL仅涉及电压和电流的加减。而支路关系可能涉及这些量对时间的微分或积分。因此,对于电感器L两端电压υL(t)和流过它的电流iL(t)满足方程:
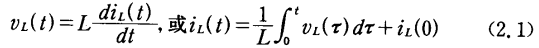
同样,对于电容C,保持关系式:
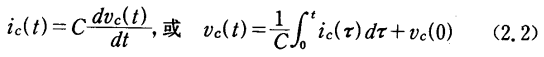
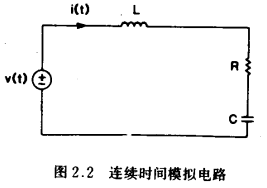
因此,电路方程一般为积分一微分关系。例如图2.2所示的电路,电流i(t)可以通过解方程
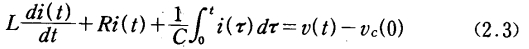
得到。为了求解,初始值i(0)和υc(0)必须已知。
这样的积分一微分方程可以直接用数学方法求解。然而,这会导致求解的复杂化。采用拉氏变换求解技术会方便得多,这将在下一节中讨论。
同样,离散时间系统的分析也涉及网络方程的建立和求解。为了建立这些方程,仅涉及加减法(类似于基尔霍夫定律)的拓扑关系必须与支路关系相结合。后者可能涉及被一个常数乘,或被一个抽样周期T延迟。作为一个例子,考虑图2.3所示的数字系统。
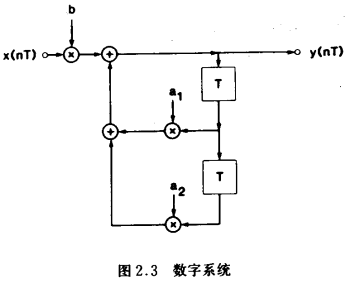
容易看到系统输入一输出间的关系为:
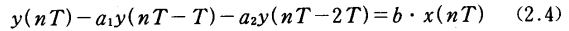
这是一个差分方程,如果给定初值y(o)和y(-T),那么可以用直接方法求解。然而,用Z变换处理会更简单,这将在2.4节中讨论。
对于一个线性时不变连续时间模拟系统,一个重要的特性是它的冲击响应。冲击函数或狄拉克函数δ(t)可以认为是图2.4所示的脉冲函数Pε(t)当ε→0时的极限情况。冲击响应h(t)是δ(t)为输入信号时(图2.5a)系统(初始状态为零时)的输出。
假如同一零状态系统的输入信号为x(t)激励[图2.5(b)),那末可以证明,该系统的输出为

这里,假定当t<0时,x(t)=h(t)=0。因此,冲击响应也能够确定系统对其它信号的响应。
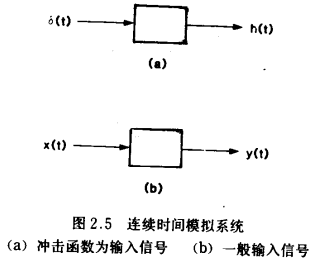
图2.5中所示的x(t)和h(t)间的运算常常用x(t)*h(t)表示,称为x(t)和h(t)的(单边)卷积。显然,除了非常简单的函数,它是一个复杂的处理过程。然而,再一次应用拉氏变换可以使这个处理过程非常容易,这将在下节中讨论。
对于线性时不变离散时间系统可以导出类似的结果。现在冲击函数定义为:
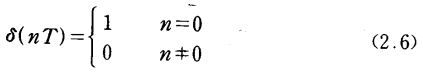
冲击响应h(nT)是δ(nT)输入时,系统(初始条件为零)的输出。
对于一个不同的输入信号x(nT),具有零初始状态系统的输出可由卷积(或卷积和[3])给出
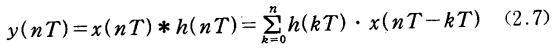
这里,假设n<0时,x(nT)=h(nT)=0.除了最简单的x(nT)和h(nT)外,直接进行这一运算是冗长繁琐的。然而,正如以后会见到的,Z变换的使用将大大减少这些必要的运算。
可以断言,采用变换方法,线性时不变系统的分析会容易得多。因此,在以后的几节中,将探讨这些技术。
联系方式:邹先生
联系电话:0755-83888366-8022
手机:18123972950
QQ:2880195519
联系地址:深圳市福田区车公庙天安数码城天吉大厦CD座5C1
请搜微信公众号:“KIA半导体”或扫一扫下图“关注”官方微信公众号
请“关注”官方微信公众号:提供 MOS管 技术帮助