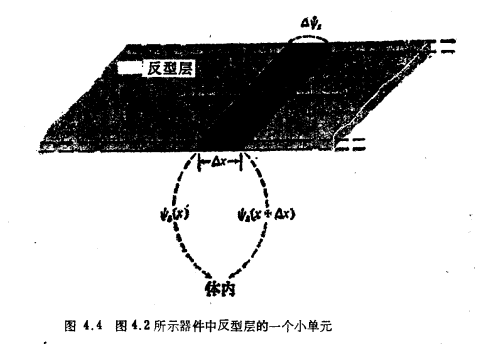
四端MOS结构通用电荷薄层模型解析在本节中,我们要推导一个适用于所有工作区的漏端电流表达式。标题中的通用二字就是对这一广泛适用性而言的。电荷薄层这一术语是指这一模型中的基本假设,即反型层具有无限小的厚度①。因为注意到在第2和第3章中已经作了这一假设,所以可把第2、3章中的表达式用到现在的推导中来。下面我们将要介绍的这种模型已在若干参考文献[53,54,56-59]中导出,但是我们的推导方法将更简单
四端MOS结构通用电荷薄层模型解析在本节中,我们要推导一个适用于所有工作区的漏端电流表达式。标题中的通用二字就是对这一广泛适用性而言的。电荷薄层这一术语是指这一模型中的基本假设,即反型层具有无限小的厚度①。因为注意到在第2和第3章中已经作了这一假设,所以可把第2、3章中的表达式用到现在的推导中来。下面我们将要介绍的这种模型已在若干参考文献[53,54,56-59]中导出,但是我们的推导方法将更简单

四端MOS结构晶体管的工作区及其特性解析晶体管的工作区一个NMOS晶体管的典型的直流电流-电压特性曲线簇示于图4.3a和b,它们分别对应于图4.2a和图4.2b。这些曲线中的细节问题将在以后讨论。一般情况下,漏端电流ID以一种复杂的方式依赖于端电压。但是在端电压的某种组合下,有可能作些简化,因而可导出相对简单的电流表达式。预先考虑到这一点,所以,我们将如表4.1中所说明的那样定义晶体管的工作区。这
四端MOS结构晶体管的工作区及其特性解析晶体管的工作区一个NMOS晶体管的典型的直流电流-电压特性曲线簇示于图4.3a和b,它们分别对应于图4.2a和图4.2b。这些曲线中的细节问题将在以后讨论。一般情况下,漏端电流ID以一种复杂的方式依赖于端电压。但是在端电压的某种组合下,有可能作些简化,因而可导出相对简单的电流表达式。预先考虑到这一点,所以,我们将如表4.1中所说明的那样定义晶体管的工作区。这

四端MOS结构基本特性及作用结构分析在第3章中的结构上再加上一端,从而使反型层在两个相对的末端处可与外界接触,这样便得到了四端MOS晶体管。在这两末端之间加上一个电压,就可在反型层中引起电流流动。由于用来导电的载流子的数目取决于栅端的电势,故当用于数字电路时,栅端电势可用来建立或消除反型层(也就是说,使器件“导通”或“截止”);当用于模拟电路时,栅端电势可用来连续地调制器件的导电性。MOS晶体管的
四端MOS结构基本特性及作用结构分析在第3章中的结构上再加上一端,从而使反型层在两个相对的末端处可与外界接触,这样便得到了四端MOS晶体管。在这两末端之间加上一个电压,就可在反型层中引起电流流动。由于用来导电的载流子的数目取决于栅端的电势,故当用于数字电路时,栅端电势可用来建立或消除反型层(也就是说,使器件“导通”或“截止”);当用于模拟电路时,栅端电势可用来连续地调制器件的导电性。MOS晶体管的

关于三端MOS结构-中反型界限的精确定义①在要求精确的情况下,中反型区的界限点可比3.2节中更为仔细地加以定义。得出这种精确定义的推理与2.7节中对二端结构的讨论相同,这里毋须重复。这种精确定义基本上是把中反型的开始点置于这样一点上,高于此点,图3.2c中曲线的斜率开始明显变化。与此类似,把中反型区的上限点置于这样一点上,在该点之下,图3.2d中曲线的斜率开始明显变化。相应的表面势的界限值ΦM和
关于三端MOS结构-中反型界限的精确定义①在要求精确的情况下,中反型区的界限点可比3.2节中更为仔细地加以定义。得出这种精确定义的推理与2.7节中对二端结构的讨论相同,这里毋须重复。这种精确定义基本上是把中反型的开始点置于这样一点上,高于此点,图3.2c中曲线的斜率开始明显变化。与此类似,把中反型区的上限点置于这样一点上,在该点之下,图3.2d中曲线的斜率开始明显变化。相应的表面势的界限值ΦM和

三端MOS结构弱反型特性函数形式现象分析对于一给定的VCB值,弱反型区定义为(图3.2):在这一区内,有现在来考虑式(3.2.6)。该式中第一个根号下的第二项的值是不大的,这是因为在弱反型区,ψs ΦM然(图3.2),并且从式(3.4.2)可知,ΦM=2ΦF+VCB。因此,和导出二端结构的式(2.5.33)一样,可以用泰勒级数展开求得Q´I:我们要提醒读者,在弱反型区内,VCB不能解释为有效反向偏
三端MOS结构弱反型特性函数形式现象分析对于一给定的VCB值,弱反型区定义为(图3.2):在这一区内,有现在来考虑式(3.2.6)。该式中第一个根号下的第二项的值是不大的,这是因为在弱反型区,ψs ΦM然(图3.2),并且从式(3.4.2)可知,ΦM=2ΦF+VCB。因此,和导出二端结构的式(2.5.33)一样,可以用泰勒级数展开求得Q´I:我们要提醒读者,在弱反型区内,VCB不能解释为有效反向偏

三端MOS结构中反型的一般关系式解析三端MOS结构中反型在图3.2中可见,对于一给定的VCB值,中反型定义为[9]与二端结构情况一样,对于中反型区未曾进行过合适的简化,故应该采用精确公式。对于一给定的ψs值,Q´I和VGB可从式(3.2.6)和(3.2.7b)求出,于是曲线Q´I(VGB)便可绘出。联系方式:邹先生联系电话:0755-83888366-8022手机:18123972950QQ:28
三端MOS结构中反型的一般关系式解析三端MOS结构中反型在图3.2中可见,对于一给定的VCB值,中反型定义为[9]与二端结构情况一样,对于中反型区未曾进行过合适的简化,故应该采用精确公式。对于一给定的ψs值,Q´I和VGB可从式(3.2.6)和(3.2.7b)求出,于是曲线Q´I(VGB)便可绘出。联系方式:邹先生联系电话:0755-83888366-8022手机:18123972950QQ:28

三端MOS结构强反型区及其特性作用解析三端MOS结构强反型从图3.2可见,对于给定的VCB值,强反型定义为:精确计算指出,虽然在深度强反型区内|Q´I|≥|Q´B|,但对于十分接近VGBH的VGB值,Q´I可大于或小于Q´B(Q´I应为|Q´I|,Q´B应为|Q´B|——译者),这取决于衬底的掺杂浓度和氧化层的厚度。决定三端结构在强反型时的真正特性的不是|Q´I|和|Q´B|值的相对大小,而是它们
三端MOS结构强反型区及其特性作用解析三端MOS结构强反型从图3.2可见,对于给定的VCB值,强反型定义为:精确计算指出,虽然在深度强反型区内|Q´I|≥|Q´B|,但对于十分接近VGBH的VGB值,Q´I可大于或小于Q´B(Q´I应为|Q´I|,Q´B应为|Q´B|——译者),这取决于衬底的掺杂浓度和氧化层的厚度。决定三端结构在强反型时的真正特性的不是|Q´I|和|Q´B|值的相对大小,而是它们

三端MOS结构反型区及其近似界限分析近似界限对于二端MOS结构,我们已用式(2.5.8)至(2.5.10)所给出的表面势值ΦL0、ΦM0和ΦH0分别定义了弱、中和强反型的开始点。基于3.2节的讨论,用如下的表面势值相应地定义三端结构的这些开始点是合理的:其中最后一式中的Φz为几个Φt,因此ψs大于ΦH后,表面势相对恒定①(见图3.2a)。并且相应的Q´I(VGB)曲线(见图2.2d)基本上为一直线
三端MOS结构反型区及其近似界限分析近似界限对于二端MOS结构,我们已用式(2.5.8)至(2.5.10)所给出的表面势值ΦL0、ΦM0和ΦH0分别定义了弱、中和强反型的开始点。基于3.2节的讨论,用如下的表面势值相应地定义三端结构的这些开始点是合理的:其中最后一式中的Φz为几个Φt,因此ψs大于ΦH后,表面势相对恒定①(见图3.2a)。并且相应的Q´I(VGB)曲线(见图2.2d)基本上为一直线

三端MOS结构体效应特性及其作用分析体效应根据上清楚可见,增加VCB将会减弱反型程度,除非把VGB也增加一适当值。且结果是,若要保持反型程度不变,VGB的增加量必须大于VCB的增加量。这一现象称为体效应或衬底效应。本节中,我们将试图提供关于体效应的直观知识。定量结果将在讨论各反型区分界点的后续各节中给出。讨论上述效应最好借助于图3.1d。体效应实际上与下面的事实有关:若图3.1d中所连接的VcB增
三端MOS结构体效应特性及其作用分析体效应根据上清楚可见,增加VCB将会减弱反型程度,除非把VGB也增加一适当值。且结果是,若要保持反型程度不变,VGB的增加量必须大于VCB的增加量。这一现象称为体效应或衬底效应。本节中,我们将试图提供关于体效应的直观知识。定量结果将在讨论各反型区分界点的后续各节中给出。讨论上述效应最好借助于图3.1d。体效应实际上与下面的事实有关:若图3.1d中所连接的VcB增

三端MOS结构及其与反型层接触解析与反型层接触假定在基本的MOS二端结构中加上一个n+区,从而得到如图3.1a所示的结构;在未作进一步说明之前,假设VGB为常数。现在来考虑n+区与衬底形成的n+p结。如图所示,p侧耗尽区包含有电离了的受主原子,n+材料中的耗尽区含有电离了的施主原子(见图1.15),因为它很狭窄,为简单起见,图中没有画出。如1.5节所指出的,可以把n+区端与衬底短路而不改变此结构,
三端MOS结构及其与反型层接触解析与反型层接触假定在基本的MOS二端结构中加上一个n+区,从而得到如图3.1a所示的结构;在未作进一步说明之前,假设VGB为常数。现在来考虑n+区与衬底形成的n+p结。如图所示,p侧耗尽区包含有电离了的受主原子,n+材料中的耗尽区含有电离了的施主原子(见图1.15),因为它很狭窄,为简单起见,图中没有画出。如1.5节所指出的,可以把n+区端与衬底短路而不改变此结构,